APPLICATION OF PRIM' s AND KRUSKAL' s ALGORITHM IN REAL-LIFE SCENARIOUS

 Welcome! Let’s start with some informal context. Let me ask you something:

            Have you ever used Google Maps for directions? Have you ever used Social Media apps like Facebook or Instagram? Well, guess what, you have been using graphs all along. Let’s see what these algorithms actually are and how they work.

If “Yes” to any of these questions, then you’ve definitely used graphs and you didn’t even know it! Surprised? I was, too! 

Through this blog, we will go through two essential, yet fun algorithms and compare them in real-world scenarios.

Let’s say our task is to find minimum path from current location to destination in such a way that we need to find out all the paths and from this we need to find minimum path and the minimum cost of path. Now how do we find that out? We can use Prim’s Algorithm or Kruskal’s Algorithm.

Both Prims and Kruskal Algorithms are used to find the minimum spanning

trees. So now, what is Minimum Spanning Tree?

MST is used to decide path which gives minimum cost to apply daily life concepts like travelling, salesman's problems, electrical wiring, etc. So here we show how minimum cost is calculated in minimum spanning tree using different algorithms like prim's and kruskal's algorithm.

 Fig : Minimum Spanning Tree

Now the applications of the Kruskal and Prims Algorithm are basically the applications of minimum spanning tree. Both approaches are known as ‘greedy’ algorithms. So now What is a ‘greedy’ algorithm?

It is called greedy because it chooses the optimal solution present at the moment and not the optimal solution as a whole. In greedy algorithms, at every step, there is a choice that is optimal for the problem up to that step, and after the last step, the algorithm produces the optimal solution of the complete problem.

Both the algorithms are two similar to minimum spanning tree. What left me wondering was when one should use Prim’s algorithm and when Kruskal’s to find the minimum spanning tree? They both have easy logics, the same worst cases, and the only difference is the implementation which might involve a bit different data structure. So what is the deciding factor?

The basic difference is in which edge you choose to add next to the spanning tree in each step.

In Prim’s algorithm, you always keep a connected component, starting with a single vertex. Prims algorithm finds minimum cost spanning tree by selecting edges from graph one by one. It starts with tree T consisting of vertex x. Then it adds shortest edges edge emanating from x that connects to T to rest of graph. It then moves further and repeat process.    

In Kruskal’s algorithm, it finds the minimum cost spanning tree of graph by adding edges one by one. However, Kruskal's algorithm form a forest of trees which are joined together incrementally to form minimum cot spanning tree. 

  

Now I recommend you all to go in the technical of both the algorithms through other blogs and learn the difference in the implementations of both.

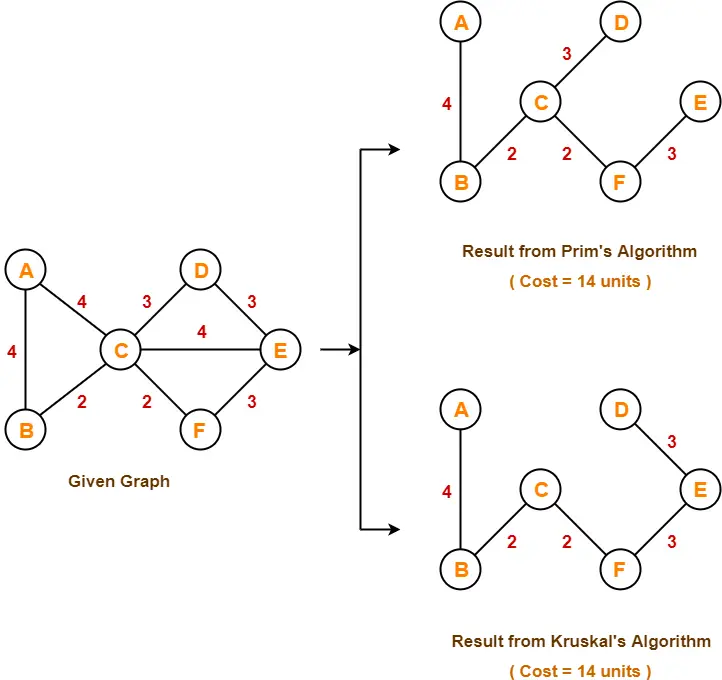
  Comparison of the two algorithms

 Minimum spanning tree application in the currency market :

1.    Currency Market 

    * Recently, a lot of authors have focused on graph-theoretical representation and analysis of the financial market.

    * Best approach: - Scientist had chosen minimum spanning tree research in currency market. Because it is best data type suitable for currency market.

2.   Social Media

    * Everyone has used social media sites. In social media we have our network i.e we connect with our friends.

    * Many a times social sites suggests us to send a connection request to a person we might know but haven’t sent the request and it also show how many mutual friends are there between you and the person you are sending the connection request.

So have you ever wondered how this works internally. Basically it uses the graph data structure 

• Applications where Kruskal’s algorithm is generally used:

1.   Landing cables

2.   TV Network

3.   Tour Operations

4.   LAN Networks

5.   A network of pipes for drinking water or natural gas.

6.   An electric grid

7.   Single-link Cluster

 

• Applications where Prim’s algorithm is generally used:

1.   All the applications stated in the Kruskal’s algorithm’s applications can be resolved using Prim’s algorithm (use in case of a dense graph).

2.   Network for roads and Rail tracks connecting all the cities.

3.   Irrigation channels and placing microwave towers

4.   Designing a fiber-optic grid or ICs.

5.   Travelling Salesman Problem.

6.   Cluster analysis.

7.   Pathfinding algorithms used in AI(Artificial Intelligence).

8.   Game Development

9.   Cognitive Science

 

       Authors

           Vishwakarma Institute Of Technology, Pune.

           Second-Year Students, Computer Department

-         Achwale Prajwal Namdevrao

-         Devshatwar Shruti Rangnath

-         Jotrao Rutuja Sanjay

-         Motbhare Subodh Uddhav

-         Shaha Shraddha Shrenikkumar